Innhold

• Steps
• Tips

Matematikere og grafikkprogrammerere trenger ofte å finne vinkelen mellom to vektorer. Heldigvis krever formelen som brukes for å beregne denne vinkelen ikke annet enn et enkelt skalarprodukt. Selv om resonnementet bak denne formelen er lettere å forstå når du bruker todimensjonale vektorer, kan vi enkelt tilpasse den til vektorer med et hvilket som helst antall komponenter.

Steps

Del 1 av 2: Beregn vinkelen mellom to vektorer

1. 

   Identifiser de to vektorene. Skriv ned all kjent informasjon om de to vektorene. I forbindelse med denne opplæringen vil vi anta at du bare kjenner vektorene når det gjelder dimensjonale koordinater (også kalt komponenter). Hvis du allerede vet det modul eller standard av disse vektorene (det vil si lengden), kan du hoppe over noen av trinnene nedenfor.
   • Eksempel: vi vil vurdere de todimensjonale vektorene = (2,2) og = (0,3). Disse to vektorene kan skrives om som = 2Jeg + 2j e = 0Jeg + 3j = 3j.
   • Selv om vårt eksempel bruker to todimensjonale vektorer, kan vi bruke følgende instruksjoner på vektorer med et hvilket som helst antall komponenter.

2. 

   
   
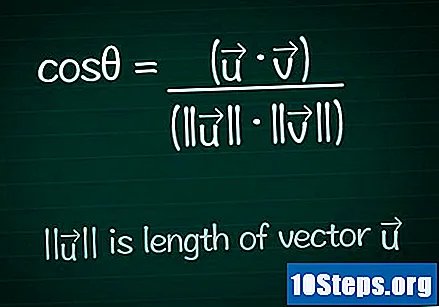
   Skriv kosinusformelen. For å finne verdien av vinkelen θ mellom to vektorer, må vi først beregne kosinus for den vinkelen. Du kan søke og finne ut formelen i detalj eller ganske enkelt skrive den slik den er nedenfor:
   • cosθ = (•) / (|||| ||||)
   • |||| representerer modul (eller lengde) på vektoren ".
   • • representerer skalar produkt (eller internt produkt) av de to vektorene.

3. 

   
   
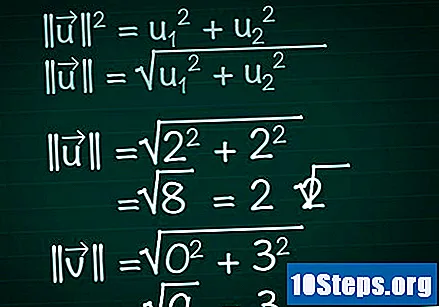
   Beregn modulen til hver vektor. Se for deg en riktig trekant dannet av komponenten x av en vektor, dens komponent y og selve vektoren. I denne trekanten spiller vektoren hypotenusen; Derfor vil vi bruke Pythagorean teorem for å finne dens lengde. Som et resultat er denne formelen lett anvendelig for vektorer med et hvilket som helst antall komponenter.
   • || u || = u₁ + u₂. Hvis vektoren har mer enn to komponenter, fortsetter du bare å legge til + u₃ + u₄ +...
   • Derfor, for en todimensjonal vektor, må vi gjøre det || u || = √ (u₁ + u₂).
   • I vårt eksempel er |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Beregn det skalare produktet mellom de to vektorene. Du bør allerede kjenne til metoden for å multiplisere vektorer, også kalt skalar produkt. For å beregne skalarproduktet til to vektorer med tanke på deres komponenter, multipliserer vi komponentene i samme retning med hverandre og legger deretter til resultatene av disse produktene.
   • Hvis du jobber med datagrafiksprogrammer, kan du først besøke delen "Tips" før du fortsetter.
   • I matematiske termer, • = u₁v₁ + u₂v₂, hvor u = (u₁, u₂). Hvis vektoren din har mer enn to komponenter, bare fortsett å legge til + u₃v₃ + u₄v₄...
   • I vårt eksempel: • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dette er verdien av det skalare produktet mellom vektorene og.

5. 

   Bytt ut disse resultatene i kosinusformelen. Husk at cosθ = (•) / (|||| || ||). Vi har allerede beregnet skalarproduktet og modulen til de to vektorene. La oss nå erstatte disse verdiene i formelen og beregne kosinusens vinkel.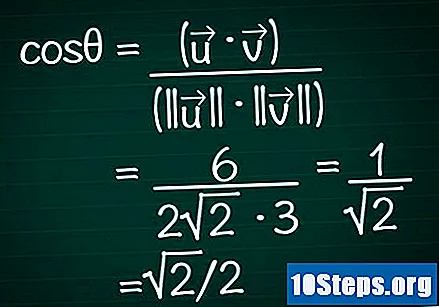
   • I vårt eksempel er cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Finn vinkelen basert på kosinus.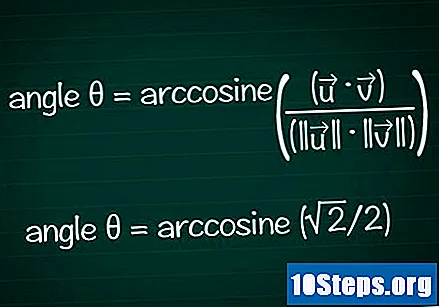
   Bruk kalkulatorens bue- eller cos-funksjon for å bestemme vinkelen θ fra din kosinusverdi. I noen tilfeller kan du være i stand til å finne vinkelverdien basert på enhetssirkelen.
   • I vårt eksempel er cosθ = √2 / 2. Skriv "arccos (√2 ​​/ 2)" i kalkulatoren for å finne vinkelen. Et annet alternativ er å se etter vinkelen θ på enhetssirkelen der cosθ = √2 / 2: dette vil stemme for θ = /₄ eller 45 °.
   • Når vi samler all informasjonen, vil vi ha den endelige formelen θ = arccosine ((•) / (|||| || ||))

Del 2 av 2: Definere formelen for beregning av vinkelen

1. 

   Forstå formålet med formelen. Formelen vi brukte for å beregne vinkelen mellom to vektorer var ikke avledet fra eksisterende regler; i stedet ble det opprettet som en definisjon av det skalære produktet mellom to vektorer og vinkelen mellom dem. Denne avgjørelsen er imidlertid ikke vilkårlig. Med en nærmere titt på grunnleggende geometri kan vi se hvorfor denne formelen resulterer i så nyttige og intuitive definisjoner.
   • Følgende eksempler bruker todimensjonale vektorer fordi de er den mest intuitive typen å jobbe med. Vektorer med tre eller flere dimensjoner har sine egenskaper definert ut fra den generelle formelen (også på en veldig lik måte).

2. 

   Gjennomgå kosinusloven. I hvilken som helst trekant, vurder vinkelen θ dannet av sidene De og B og siden ç motsatt den vinkelen. I følge kosinusloven er c = a + b -2ablinning(Θ). Demonstrasjonen av denne formelen kan lett oppnås fra kunnskap om grunnleggende geometri.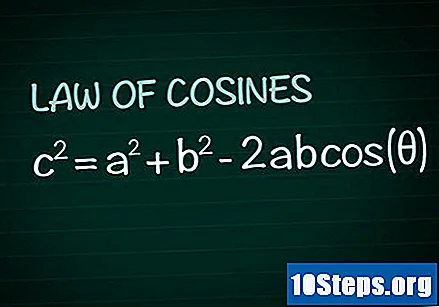

3. 

   Koble de to vektorene til å danne en trekant. Tegn et par vektorer, og med en vinkel θ mellom dem. Deretter tegner du en tredje vektor mellom dem for å danne en trekant. Med andre ord tegne vektoren slik at + =, eller ganske enkelt = -.

4. 

   Bruk kosinusloven på denne trekanten. Bytt ut lengden på sidene på vår vektor trekant (det vil si vektormodulen) i formelen for kosinusloven:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||linning(θ)

5. 

   Omskriv formelen ved å bruke skalare produkter. Husk at prikkproduktet er utvidelsen av en vektor projisert på en annen. Det skalare produktet til en vektor i seg selv krever ikke projeksjon fordi det ikke er noen retningsendring. Dette betyr at • = || a ||. Basert på denne informasjonen, la oss skrive om ligningen til kosinusloven:
   • (-) • (-) = • + • - 2 || a || || b ||linning(θ)

6. 

   Forenkle formelen. Utvid produktene på venstre side av ligningen og forenkle det til du kommer til formelen vi kjenner for å beregne vinkler.
   • • - • - • + • = • + • - 2 || a || || b ||linning(θ)
   • - • - • = -2 || a || || b ||linning(θ)
   • -2 (•) = -2 || a || || b ||linning(θ)
   • • = || a || || b ||linning(θ)

Tips

• For rask oppløsning, bruk følgende formel på ethvert todimensjonalt vektorpar: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Hvis du jobber med datagrafiksprogrammer, vil du sannsynligvis trenge å vite bare retningen til vektorene, ikke lengden. Følg trinnene nedenfor for å forenkle likningene og få fart på programmet ditt:
  • Normaliser hver vektor, det vil si, finn enhetsvektoren som har samme retning som den opprinnelige vektoren. For å gjøre dette, del hver komponent i vektoren med vektormodulen.
  • Beregn skalærproduktet til de normaliserte vektorene, ikke de opprinnelige vektorene.
  • Siden modulen (det vil si lengden) til de normaliserte vektorene er enhetlig, kan vi la dem ligge utenfor formelen. Din endelige ligning for å beregne vinkler vil være buer (•).
• Basert på formelen til kosinusloven kan vi raskt finne ut om den aktuelle vinkelen er akutt eller stump. Start med cosθ = (•) / (|||| ||||):
  • Venstre og høyre side av ligningen må ha det samme tegnet (positivt eller negativt).
  • Siden lengdene alltid er positive, vil cosθ alltid ha det samme tegnet som det skalære produktet.
  • Derfor, hvis det skalære produktet er positivt, vil cosθ være positivt. Dette betyr at vinkelen er i den første kvadranten av enhetssirkelen, det vil si θ <π / 2 eller 90 °. Derfor er vinkelen akutt.
  • Hvis det skalære produktet er negativt, er cosθ negativt. Dette betyr at vinkelen er i den andre kvadranten av enhetssirkelen, det vil si π / 2 <θ ≤ π eller 90 ° <θ ≤ 180 °. Derfor er vinkelen stump.