Innhold

• Fremgangsmåte

I fysikk er spenning den kraften som utøves av et tau, ledning, kabel eller lignende gjenstand på en eller flere gjenstander. Alt som henger, trekkes eller henges opp av et tau, kabel, wire etc. er utsatt for spenning. Som enhver kraft kan stress akselerere gjenstander eller forårsake deformasjon. Å vite hvordan man beregner stress er en viktig ferdighet ikke bare for fysikkstudenter, men også for ingeniører og arkitekter som, for å garantere sikkerheten til konstruksjonene, må vite om spenning i et tau eller kabel kan tåle deformasjonen forårsaket av vekten av objektet for å gi og bryte. Følg trinn 1 for å lære å beregne stress i forskjellige fysikksystemer.

Fremgangsmåte

Metode 1 av 2: Bestemme spenning på en enkelt ledning

1. 

   
   
   Sett kreftene på begge sider av tauet. Spenningen i et tau er et resultat av krefter som trekker tauet på begge sider. For ordens skyld, "kraft = masse × akselerasjon". Siden tauet er tett strukket, vil enhver endring i akselerasjonen eller massen av gjenstander som støttes av tauet føre til en endring i spenningen. Ikke glem den konstante akselerasjonen på grunn av tyngdekraften: selv om et system er i balanse, er dets komponenter utsatt for den kraften. Vi kan tenke på spenningen i en streng som T = (m × g) + (m × a), hvor "g" er tyngdeakkelerasjonen i ethvert objekt som trekkes av tauet og "a" er en hvilken som helst annen akselerasjon i de samme objektene.
   • I fysikk, i de fleste problemer, anser vi det som en "ideell tråd". Med andre ord, tauet vårt er tynt, uten masse og strekker seg ikke eller knekker.
   • La oss som et eksempel se på et system der en vekt blir hengt opp av en trebjelke ved hjelp av et enkelt tau (se figur). Verken vekten eller tauet beveger seg: systemet er i balanse. Vi vet at for at vekten skal holdes i balanse, må strekkraften være lik tyngdekraften i vekten. Med andre ord, Voltage (F_t) = Tyngdekraft (F_g) = m × g.
     • Med tanke på en vekt på 10 kg, er strekkfastheten 10 kg × 9,8 m / s = 98 Newton.

2. 

   
   
   Vurder akselerasjon. Tyngdekraften er ikke den eneste kraften som påvirker spenningen til et tau. Enhver akselerasjonskraft relatert til gjenstanden festet til tauet forstyrrer resultatet. Hvis for eksempel en suspendert gjenstand akselereres av en kraft på tauet, blir akselerasjonskraften (masse × akselerasjon) lagt til spenningen forårsaket av gjenstandens vekt.
   • La oss si at i vårt eksempel på vekten på 10 kg suspendert av et tau, i stedet for å bli festet på en trebjelke, blir tauet brukt til å heve denne vekten til en akselerasjon på 1 m / s. I dette tilfellet må vi vurdere akselerasjonen av vekten, samt tyngdekraften, og løse som følger:
     • F_t = F_g + m × a
     • F_t = 98 + 10 kg × 1 m / s
     • F_t = 108 Newton.

3. 

   
   
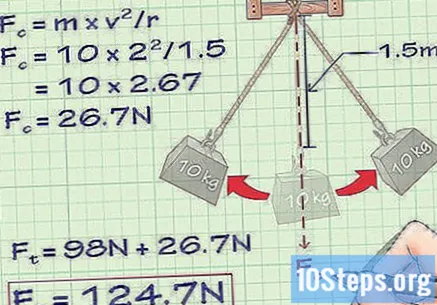
   Vurder rotasjonsakselerasjon. Et objekt som roterer rundt sitt sentrale punkt gjennom en streng (som en pendel) utøver deformasjon på strengen forårsaket av sentripetalkraften. Sentripetalkraften er den ekstra strekkraften som tauet utøver når du trekker gjenstanden mot sentrum. Dermed forblir objektet i en buebevegelse, ikke i en rett linje. Jo raskere objektet beveger seg, jo større er sentripetalkraften. Sentripetal kraft (F_ç) er lik m × v / r der "m" er masse, "v" er hastighet og "r" er radiusen til sirkelen som inneholder buen der objektet beveger seg.
   • Siden retningen og størrelsen på sentripetalkraften endres når gjenstanden som er hengt opp av et tau beveger seg og endrer hastigheten, endres også den totale spenningen i tauet, som alltid virker i retningen definert av ledningen, med en sans i sentrum. Husk alltid at tyngdekraften kontinuerlig virker på gjenstanden ved å trekke den ned.Så hvis et objekt roterer eller svir vertikalt, er den totale spenningen større på den nederste delen av buen (for en pendel kalles dette likevektspunktet) når objektet beveger seg raskere og mindre på toppen av buen, når det beveger seg saktere.
   • La oss si at objektet vårt ikke lenger akselereres oppover i vårt eksempelproblem, men det svinger som et pendel. Dette tauet er 1,5 meter langt og vekten beveger seg med 2 m / s når det passerer gjennom det laveste punktet på banen. Hvis vi ønsker å beregne spenningen på det laveste punktet i buen (når den når den høyeste verdien), må vi først erkjenne at spenningen på grunn av tyngdekraften på dette punktet er den samme som når vekten ble suspendert uten bevegelse: 98 Newton . For å finne den ekstra sentripetale kraften, vil vi løse den på følgende måte:
     • F_ç = m × v / r
     • F_ç = 10 × 2/1.5
     • F_ç = 10 × 2,67 = 26,7 Newton.
     • Derfor vil vår totale spenning være 98 + 26,7 = 124,7 Newton.

4. 

   Legg merke til at spenningen på grunn av tyngdekraften endres gjennom buen som dannes av objektets bevegelse. Som nevnt ovenfor endres både retningen og størrelsen på sentripetalkraften når objektet beveger seg i sin vei. Imidlertid, selv om tyngdekraften forblir konstant, endres også "spenningen som følge av tyngdekraften". Når et objekt ikke er på det laveste punktet i buen (likevektspunktet), trekker tyngdekraften det rett ned, men spenningen trekker det opp og danner en viss vinkel. På grunn av dette må spenningen bare nøytralisere en del av tyngdekraften, og ikke dens helhet.
   • Å dele gravitasjonskraften i to vektorer kan hjelpe deg med å visualisere dette konseptet. Når som helst i buen til et objekt som svinger vertikalt, danner strengen en vinkel θ med linjen til likevektspunktet og det sentrale rotasjonspunktet. Når pendelen svinger, kan gravitasjonskraften (m × g) deles i to vektorer: mgsen (θ) - virker tangent til buen, i retning av likevektspunktet; mgcos (θ) som virker parallelt med strekkraften i motsatt retning. Spenningen må nøytralisere mgcos (θ), kraften som trekker i motsatt retning, og ikke den totale gravitasjonskraften (unntatt i likevektspunktet, når de to kreftene er like).
   • La oss si at når pendelen vår danner en vinkel på 15 grader med vertikalen, beveger den seg på 1,5 m / s. Vi vil finne spenning ved å følge disse trinnene:
     • Stress på grunn av tyngdekraften (T_g) = 98cos (15) = 98 (0,96) = 94,08 Newton
     • Sentripetal kraft (F_ç) = 10 × 1,5 / 1,5 = 10 × 1,5 = 15 Newton
     • Totalt stress = T_g + F_ç = 94,08 + 15 = 109.08 Newton.

5. 

   Beregn friksjon. Ethvert objekt, dratt av et tau som har en motstandskraft generert av friksjonen av en gjenstand mot en annen (eller væske), overfører den kraften til spenningen i tauet. Friksjonskraften mellom to objekter beregnes som i enhver annen situasjon - etter denne ligningen: Kraft på grunn av friksjon (vanligvis representert av F_på) = (μ) N, der μ er friksjonskoeffisienten mellom to objekter og N er den normale kraften mellom to objekter, eller den kraften de utøver på hverandre. Vær oppmerksom på at statisk friksjon, som skyldes å prøve å sette et statisk objekt i bevegelse, er forskjellig fra dynamisk friksjon, som skyldes å prøve å holde et objekt i bevegelse.
   • La oss si at vekten på 10 kg ikke lenger blir påvirket, men blir dratt horisontalt langs en flat overflate av tauet vårt. Med tanke på at overflaten har en dynamisk friksjonskoeffisient på 0,5 og vekten vår beveger seg med konstant hastighet, vil vi akselerere den til 1 m / s. Dette nye problemet presenterer to viktige endringer: for det første trenger vi ikke lenger å beregne spenningen på grunn av tyngdekraften, fordi vekten ikke blir suspendert av tauet. For det andre må vi beregne spenningen forårsaket av friksjon, så vel som den forårsaket av akselerasjonen av massen av den vekten. Vi må løse følgende:
     • Normal kraft (N) = 10 kg × 9,8 (tyngdekraftsakselerasjon) = 98 N
     • Dynamisk friksjonskraft (F_atd) = 0,5 × 98 N = 49 Newton
     • Akselerasjonskraft (F_De) = 10 kg × 1 m / s = 10 Newton
     • Totalt stress = F_atd + F_De = 49 + 10 = 59 Newton.

Metode 2 av 2: Beregning av flere strengstress

1. 

   Trekk hengende last vertikalt og parallelt med en remskive. Remskiver er enkle maskiner, som består av en hengende plate som lar spenningskraften endre retning. I en enkel remskivekonfigurasjon går tauet eller kabelen langs remskiven, med vekter festet i begge ender, og skaper to segmenter av tau eller kabel. Spenningen i begge ender av tauet er imidlertid den samme, selv om de blir trukket av krefter av forskjellige størrelser. I et system med to masser suspendert av en vertikal remskive, er spenningen lik 2g (m₁) (m₂) / (m₂+ m₁), hvor "g" er tyngdeakselerasjonen, "m₁"er massen av objekt 1, og" m₂"er massen av objekt 2.
   • Legg merke til at fysikkproblemer generelt vurderer "ideelle remskiver": uten masse, uten friksjon, som ikke kan knekke, deformere eller løsne seg fra taket eller tauet som henger den.
   • La oss si at vi har to vekter suspendert vertikalt fra en remskive med parallelle tau. Vekt 1 har en masse på 10 kg, mens vekt 2 har en masse på 5 kg. I dette tilfellet vil vi finne spenningen slik:
     • T = 2g (m₁) (m₂) / (m₂+ m₁)
     • T = 2 (9,8) (10) (5) / (5 + 10)
     • T = 19,6 (50) / (15)
     • T = 980/15
     • T = 65.33 Newton.
   • Merk at fordi en vekt er tyngre enn en annen, og alle andre ting er likeverdige, vil dette systemet akselerere, med vekten på 10 kg som beveger seg nedover og vekten på 5 kg beveger seg oppover.
2. Gjør beregninger for belastninger hengende av en remskive med ikke-parallelle vertikale tau. Remskiver brukes ofte til å lede spenning i en retning, i stedet for opp eller ned. Hvis for eksempel en vekt er suspendert vertikalt på den ene enden av tauet, mens den andre enden er koblet til en annen vekt i en diagonal skråning, tar det ikke-parallelle remskivesystemet form av en trekant, med punkter på den første og andre vekt og remskive. I dette tilfellet påvirkes spenningen i tauet både av tyngdekraften i vekten og av komponenten av kraften som er parallell med tauets diagonale del.
   • La oss si at vi har et system med en vekt på 10 kg (m₁) hengt vertikalt og koblet gjennom en remskive til en vekt på 5 kg (m₂) på en 60 graders rampe (forutsatt at rampen ikke har noen friksjon). For å finne spenningen i strengen er det lettere å finne ligningene for kreftene som akselererer vektene først. Følg disse instruksjonene:
     • Den opphengte vekten er tyngre, og vi vurderer ikke friksjon; derfor vet vi at den vil akselerere nedover. Til tross for spenningen i tauet som trekker vekten opp, akselererer systemet på grunn av den resulterende kraften F = m₁(g) - T, eller 10 (9.8) - T = 98 - T.
     • Vi vet at vekten på rampen vil akselerere oppover. Siden rampen ikke har noen friksjon, vet vi at spenningen trekker deg opp rampen og "bare" din egen vekt trekker den ned. Den nedadgående kraftkomponenten er gitt av mgsen (θ), så i vårt tilfelle kan vi ikke si at den akselererer opp rampen på grunn av den resulterende kraften F = T - m₂(g) sen (60) = T - 5 (9,8) (0,87) = T - 42,14.
     • Akselerasjonen av de to vektene er ekvivalent. Så vi har (98 - T) / m₁ = (T - 42,63) / m₂. Etter en triviell jobb for å løse ligningen, kommer vi til resultatet av T = 60,96 Newton.

3. 

   Tenk på flere strenger når du løfter en vekt. Til slutt, la oss vurdere et objekt som er suspendert fra et strengsystem i form av en Y: to strenger festet til taket, som er på et sentralt punkt, der en vekt er suspendert av en tredje streng. Spenningen i den tredje strengen er åpenbar: det er ganske enkelt spenningen som skyldes tyngdekraften, eller m (g). De resulterende spenningene i de to andre strengene er forskjellige og må ha en sum lik gravitasjonskraften med vertikal retning oppover og lik null i begge horisontale retninger, forutsatt at systemet er i likevekt. Spenningen i strengene påvirkes både av massen til den suspenderte gjenstanden og vinkelen der hver streng er i taket.
   • La oss si at bunnvekten i vårt Y-formede system har en masse på 10 kg og de to øverste strengene møtes i taket, i en vinkel på henholdsvis 30 og 60 grader. Hvis vi vil finne spenningen i hver av de øvre strengene, må vi ta i betraktning de vertikale og horisontale komponentene i hver spenning. I dette eksemplet er de to strengene likevel vinkelrette på hverandre, noe som gjør det enkelt å beregne i henhold til definisjonene av følgende trigonometriske funksjoner:
     • Forholdet mellom T = m (g) og T₁ eller T₂ og T = m (g) er lik sinusen til vinkelen mellom hvert støttetau og taket. For deg₁, sinus (30) = 0,5, og for T₂, sinus (60) = 0,87
     • Multipliser spenningen i den nedre strengen (T = mg) med sinusen i hver vinkel for å finne T₁ og T₂.
     • T₁ = 5 × m (g) = 5 × 10 (9.8) = 49 Newton.
     • T₁ = 87 × m (g) = 87 × 10 (9.8) = 85.26 Newton.